该篇为初学时,在阅读李航老师的《统计学习方法中》进行的一些摘录。主要是介绍机器学习的一些基本概念。
该篇部分内容转自adamlay的博客。
该篇有很多东西讲的很好。
三要素
方法=模型+策略+算法。上篇未有太多赘述,本篇做一个简单的解释。
总的来说模型、策略和算法三者之间的关系就相当于,给你一张试卷去学习,使用什么样的方法去学习试卷上题目的规律、解题思路的过程就是模型;学习所得与标准答案之间差多少,如何来计算评估这种差值就是策略;最后反馈给模型得到最优的结果就是算法。
1.模型
所有有可能的条件概率或决策函数。模型的决策空间包含所有有可能的条件概率或决策函数。
2.策略
本质:考虑按照什么样的准则学习和选择最优的模型。
1)损失函数和风险函数
- 0-1损失函数
- 平方损失函数
- 绝对损失函数
- 对数损失函数
损失函数越小,模型就越好。
输入输出遵循联合分布,我们可以求出损失函数的期望,平均意义下的损失,称为风险函数(risk function)或期望损失(expected loss)
目的:选择期望风险最小的模型。
给定一个训练数据集,求出平均损失->经验损失(empirical risk)、经验损失(empirical loss)
大数定律:当数据特别多时,经验损失逼近风险函数。
2)经验风险最小化与结构风险最小化
本质:由于数据往往没有那么多,所以用经验损失估计期望损失结果并不理想,要对经验风险进行一定的校正。
经验风险最小化:经验风险最小的模型就是最优的模型。
例子:最大似然估计。
缺点:样本容量很小时,会出现“过拟合”的现象。
结构风险最小化:添加正则化项(regularization)或罚项(penalty term)
例子:贝叶斯估计
3.算法
数值计算方法找出最优解。
模型评估与模型选择
1.训练误差和测试误差
测试误差更小具有更好的预测能力,是更有效的方法。通常将学习方法对未知数据的预测能力称为泛化能力。
2.模型选择
1.正则化
在经验风险上加上一个由模型复杂度确定正则化项。选择复杂度较小的模型。
2.交叉验证
用于数据不足的时候
1.简单交叉验证
将数据分为两部分:一部分作为训练集,一部分作为测试集。
2.S折交叉验证
首先随机地将已给的数据切分为S个互不相交的大小相同的子集,然后利用S-1个子集的数据训练数据,利用余下的子集作为测试模型。将这一过程对可能的S种选择重复进行。最后选出S次评测种平均测试误差最小的模型,
3.留一交叉验验证
S折交叉验证的特殊情形S=N,称为留一交叉验证。N是给定数据集的容量。
过拟合和欠拟合(重要)
先来一句易懂的话:
过拟合简单来说就是模型把训练集的东西学得太精了,对未知的数据效果却很差(打个比方就是考前你练得很不错,给啥做过的题都说得出答案,但是考试的时候碰到新题了就做得很差) 。
欠拟合就是模型学得很差,打个比方就是考前有题给你练,你也练了,但就是练不会,学不懂。
下面是具体介绍:
当假设空间中含有不同复杂度的模型时,就要面临**模型选择(model selection)**的问题。
我们希望获得的是在新样本上能表现得很好的学习器。为了达到这个目的,我们应该从训练样本中尽可能学到**适用于所有潜在样本的”普遍规律”**。
我们认为假设空间存在这种”真”模型,那么所选择的模型应该逼近真模型。
拟合度可简单理解为模型对于数据集背后客观规律的掌握程度,模型对于给定数据集如果拟合度较差,则对规律的捕捉不完全,用作分类和预测时可能准确率不高。
换句话说,当模型把训练样本学得太好了的时候,很可能已经把训练样本自身的一些特点当作了所有潜在样本的普遍性质,这时候所选的模型的复杂度往往会比真模型更高,这样就会导致泛化性能下降。这种现象称为过拟合(overfitting)。可以说,模型选择旨在避免过拟合并提高模型的预测能力。
与过拟合相对的是**欠拟合(underfitting)**,是指模型学习能力低下,导致对训练样本的一般性质尚未学好。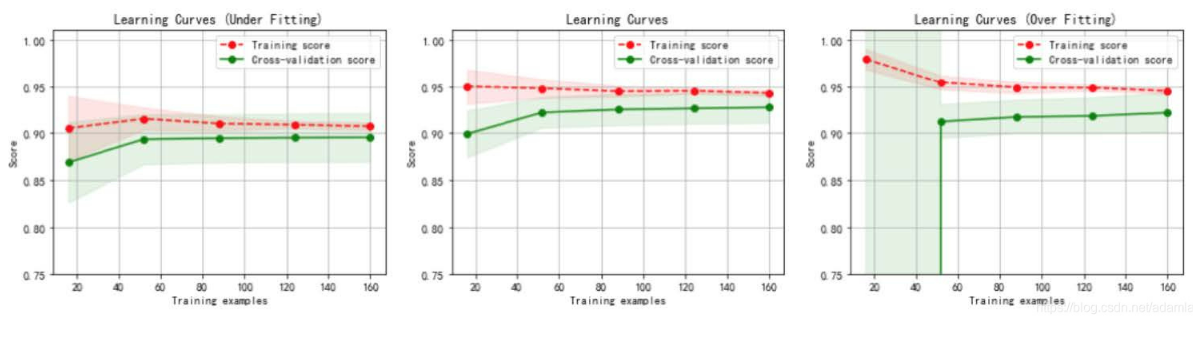
虚线:针对训练数据集计算出来的分数,即针对训练数据集拟合的准确性。
实线:针对交叉验证数据集计算出来的分数,即针对交叉验证数据集预测的准确性。
左图:一阶多项式,欠拟合;
- 训练数据集的准确性(虚线)和交叉验证数据集的准确性(实线)靠得很近,总体水平比较高。
- 随着训练数据集的增加,交叉验证数据集的准确性(实线)逐渐增大,逐渐和训练数据集的准确性(虚线)靠近,但其总体水平比较低,收敛在 0.88 左右。
- 训练数据集的准确性也比较低,收敛在 0.90 左右。
- 当发生高偏差时,增加训练样本数量不会对算法准确性有较大的改善。
中图:三阶多项式,较好地拟合了数据集;
- 训练数据集的准确性(虚线)和交叉验证数据集的准确性(实线)靠得很近,总体水平比较高。
右图:十阶多项式,过拟合。
- 随着训练数据集的增加,交叉验证数据集的准确性(实线)也在增加,逐渐和训练数据集的准确性 训练数据集的准确性很高,收敛在 0.95 左右。
- 交叉验证数据集的准确性值却较低,最终收敛在 0.91 左右。
从图中我们可以看出,对于复杂数据,低阶多项式往往是欠拟合的状态,而高阶多项式则过分捕捉噪声数据的分布规律,而噪声之所以称为噪声,是因为其分布毫无规律可言,或者其分布毫无价值,因此就算高阶多项式在当前训练集上拟合度很高,但其捕捉到的无用规律无法推广到新的数据集上。因此该模型在测试数据集上执行过程将会有很大误差,即模型训练误差很小,但泛化误差很大。
泛化能力
本质:该方法学习到的模型对未知数据的预测能力。
1.泛化误差
来评价学习方法的泛化能力。
2.泛化误差上界
学习方法的泛化能力往往是通过研究泛化误差的概率上界进行的。
泛化误差是样本容量的函数,容量增加时,泛化上界趋向于0。
泛化误差是空间容量的函数,空间容量越大,模型就越难学,泛化误差上界就越大。